materi lengkap induksi matematika, pengertian, contoh soal, induksi matematika kelas 11 Sma kurikulum 2013
Jalan Badak
Assalamualaikum
Halo sahabat jalan badak !
kali ini admin akan berbagi kiriman tentang salah satu materi matematika wajib kelas 11 Sma kurikulum 2013. Materi kali ini yaitu, induksi matematika. Pada bab ini diajarkan tentang pembuktian, bukan Cuma janji janji belaka (baperan nih adminnya wkwkwk). Yuk untuk lebih jelasnya.
baca juga : 15 website penyedia jurnal gratis terbaik
Halo sahabat jalan badak !
kali ini admin akan berbagi kiriman tentang salah satu materi matematika wajib kelas 11 Sma kurikulum 2013. Materi kali ini yaitu, induksi matematika. Pada bab ini diajarkan tentang pembuktian, bukan Cuma janji janji belaka (baperan nih adminnya wkwkwk). Yuk untuk lebih jelasnya.
baca juga : 15 website penyedia jurnal gratis terbaik
Apa itu Induksi Matematika ?
Induksi matematika merupakan suatu metode untuk membuktikan kebenaran suatu rumus atau pernyataan matematika untuk n bilangan asli.
Induksi matematika merupakan suatu metode untuk membuktikan kebenaran suatu rumus atau pernyataan matematika untuk n bilangan asli.
Untuk lebih mudah dan ada gambaran, admin kasih misal,
1+2+3+4+...+n = n(n+1) / 2
Apakah pernyataan tersebut benar ?
kita coba memasukkan n = 2 apakah hasilnya adalah 2 ?
kita coba memasukkan n = 2 apakah hasilnya adalah 2 ?
2(2+1) / 3 = 2 ternyata benar
Kita coba masukkan n
= 5
5(5+1) / 2 = 15 ternyata benar, 1+2+3+4+5 = 15
Kita coba lagi n = 10
10(10+1)/2 = 55, ternyata benar lagi (coba cek dahulu biar
tahu)
Nahh, apakah dengan membuktikan dengan 3 angka tersebut bisa
diterima secara umum atau keseluruhan? Pernyataan tersebut diaanggap sepenuhnya benar untuk
n bilangan asli? Belum. Untuk itu, perlu dibuktikan kebenarannya. Muncullah induksi
matematika. Ada 3 tahapan untuk membuktikan kebenaran suatu rumus atau pernyataan matematika menggunakan induksi matematika, yaitu :
1.) Dibuktikan untuk n = 1
2.) Dibuktikan untuk n = k
3.) Dibuktikan untuk n = k+1
baca juga : mending pilih ipa atau ips?
1.) Dibuktikan untuk n = 1
2.) Dibuktikan untuk n = k
3.) Dibuktikan untuk n = k+1
baca juga : mending pilih ipa atau ips?
Ketika anda ingin mengetahui kebenaran suatu rumus, maka kamu bisa menggunakan cara tersebut. Berikut akan saya berikan beberapa contoh :
1. )buktikan 8+11+14+17+...+(3n +5) = 1/2 n (3n+13)
Jawab :
a.) Dibuktikan F(n) berlaku untuk n = 1
(3n +5) = 1/2 (3n+13)
(3 ×1 + 5) = 1/2 × 1 (3×1 + 13)
(3+5) = 1/2 (3 + 13)
8 = 1/2 (16)
8 = 8
# F(n) benar untuk n = 1
b.) F(n) dianggap benar untuk n =k
8+11+14+17+...+(3n +5) = 1/2 n (3n+13)
8+11+14+17+...+(3k +5) = 1/2 k (3k+13)
c.) Akan dibuktikan F(n) benar untuk n = k+1
8+11+14+17+...+(3k +5) = 1/2 k (3k+13)
8+11+14+17+...+(3k +5) + (3(k+1) +5) = 1/2 (k+1) (3(k+1) +13)
1/2 k (3k +13) +(3k +8) = 1/2 (k+1) (3k+16)
1/2 ×3k² +13/2 k + 3k +8 =
1/2 (3k² + 13k + 6k + 16) =
1/2 (3k +6) (k+1)
S(n) benar untuk n = k+1
S(n) benar dan berlaku untuk n semua bilangan asli
Baca Juga : Materi Lengkap Barisan dan Deret Aritmatika kurikulum 2013
baca juga : materi lengkap glb dan glbb
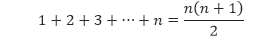
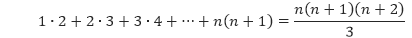
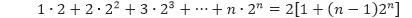
Nah, bagaimana mudah kan, untuk membuktikan suatu pernyataan matematika ? Kalo kamu merasa belum cukup paham, kamu bisa berlatih dengan soal lainnya, lalu tanyakan kepada gurumu apakah sudah benar atau belum.
Terima kasih sudah berkunjung di blog jalan badak, saya juga bukan dewa dalam matematika :D, kita disini sama sama belajar. Jadi, kalo ada kurangnya mohon dibenarkan, atau dikoreksi. Kamu bisa mengutarakan kritik, saran, dan masukkan di kolom komentar yaa
1. )buktikan 8+11+14+17+...+(3n +5) = 1/2 n (3n+13)
Jawab :
a.) Dibuktikan F(n) berlaku untuk n = 1
(3n +5) = 1/2 (3n+13)
(3 ×1 + 5) = 1/2 × 1 (3×1 + 13)
(3+5) = 1/2 (3 + 13)
8 = 1/2 (16)
8 = 8
# F(n) benar untuk n = 1
b.) F(n) dianggap benar untuk n =k
8+11+14+17+...+(3n +5) = 1/2 n (3n+13)
8+11+14+17+...+(3k +5) = 1/2 k (3k+13)
c.) Akan dibuktikan F(n) benar untuk n = k+1
8+11+14+17+...+(3k +5) = 1/2 k (3k+13)
8+11+14+17+...+(3k +5) + (3(k+1) +5) = 1/2 (k+1) (3(k+1) +13)
1/2 k (3k +13) +(3k +8) = 1/2 (k+1) (3k+16)
1/2 ×3k² +13/2 k + 3k +8 =
1/2 (3k² + 13k + 6k + 16) =
1/2 (3k +6) (k+1)
S(n) benar untuk n = k+1
S(n) benar dan berlaku untuk n semua bilangan asli
Baca Juga : Materi Lengkap Barisan dan Deret Aritmatika kurikulum 2013
baca juga : materi lengkap glb dan glbb
2.) Buktikan bahwa untuk setiap bilangan bulat positif n,
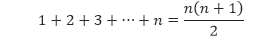
Pembahasan Misalkan P(n) adalah pernyataan 1 + 2 + 3 + … + n = n(n + 1)/2. Kita akan menunjukkan bahwa P(n) bernilai benar untuk semua bilangan bulat positif n.
- Kita harus menunjukkan bahwa P(1) benar. Dari rumus di atas, pernyataan P(1) menyatakan

dan pernyataan ini dengan jelas bernilai benar. - Anggap bahwa P(k) benar. Sehingga hipotesis induksi kita adalah
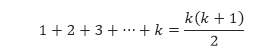
Kita akan gunakan hipotesis tersebut untuk menunjukkan bahwa P(k + 1) benar, yaitu
Sehingga, kita mulai dengan ruas kiri dan menggunakan hipotesis induksi untuk memperoleh bentuk pada ruas kanan.
Sehingga kebenaran P(k + 1) mengikuti kebenaran P(k), dan kita telah melakukan langkah induksi.
Setelah membuktikan Langkah 1 dan 2, kita dapat menyimpulkan dengan Prinsip Induksi Matematika bahwa P(n) benar untuk semua bilangan bulat positif n.
3.) Buktikan bahwa
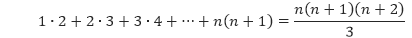
untuk semua bilangan bulat positif n.
Pembahasan Misalkan P(n) adalah pernyataan 1 ∙ 2 + 2 ∙ 3 + 3 ∙ 4 + … + n(n + 1) = [n(n + 1)(n + 2)]/3.
- Kita akan tunjukkan bahwa P(1) bernilai benar. Berdasarkan rumus di atas, P(1) menyatakan
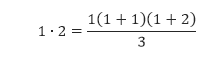
yang bernilai benar. - Anggap bahwa P(k) benar dan kita memperoleh hipotesis induksi sebagai berikut.
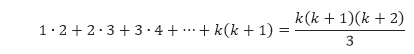
Hipotesis ini akan kita gunakan untuk membuktikan bahwa P(k + 1) benar. Pernyataan P(k + 1) menyatakan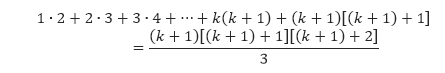
Kita mulai dari bentuk yang berada di ruas kiri, kemudian kita gunakan hipotesis induksi untuk mendapatkan bentuk pada ruas kanan.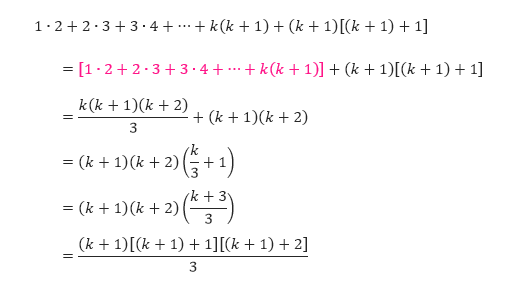
Sehingga kita telah menunjukkan bahwa P(k + 1) mengikuti P(k). Sehingga kita telah membuktikan langkah induksi.
Berdasarkan Langkah 1 dan 2, kita dapat menyimpulkan dengan menggunakan induksi matematika bahwa P(n) benar untuk semua bilangan bulat positif n.
4.) Buktikan bahwa
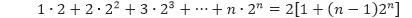
untuk semua bilangan bulat positif n.
Pembahasan Misalkan P(n) adalah pernyataan 1 ∙ 2 + 2 ∙ 2² + 3 ∙ 23 + … + n ∙ 2n = 2[1 + (n – 1)2n]
- Pertama kita buktikan bahwa P(1) benar. Pernyataan ini menyatakan
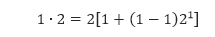
yang dengan jelas bernilai benar. - Selanjutnya, kita anggap bahwa P(k) bernilai benar dan menghasilkan hipotesis induksi sebagai berikut.
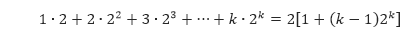
Hipotesis induksi tersebut akan kita gunakan untuk membuktikan kebenaran P(k + 1). Pernyataan P(k + 1) mengatakan
Kita mulai dari ruas kiri, kemudian kita gunakan hipotesis induksi untuk mendapatkan bentuk yang berada di ruas kanan.
Sehingga pada Langkah 2 ini kita telah membuktikan bahwa jika P(k) benar maka P(k + 1) juga benar.
sumber soal : https://yos3prens.wordpress.com/2015/10/24/25-soal-dan-pembahasan-induksi-matematika/2/
Nb : untuk lebih banyak soal lagi, kamu bisa mengunjungi blog tersebut.
Terima kasih sudah berkunjung di blog jalan badak, saya juga bukan dewa dalam matematika :D, kita disini sama sama belajar. Jadi, kalo ada kurangnya mohon dibenarkan, atau dikoreksi. Kamu bisa mengutarakan kritik, saran, dan masukkan di kolom komentar yaa
Demikian ulasan dari blog Jalan Badak semoga bermanfaat
Salam Jalan Badak
baca juga adifani.net
baca juga : biaya hidup dan kuliah di PNJ terbaru
baca juga : prinsip kerja boiler
baca juga adifani.net
baca juga : biaya hidup dan kuliah di PNJ terbaru
baca juga : prinsip kerja boiler
Amar ganteng
ReplyDeleteTerimakasih membantu sekali untuk belajar 😍
ReplyDeleteTerima kasih kaa, sangatembantuuu 😍
ReplyDelete